Partition
目前我分为二分和三分两类问题。
大部分这一类问题都是要求in-place,O(n)空间没什么意义,显然。
一般是O(n)/O(1)的复杂度
二分
Partition Array II
和前面不太一样的是,这里面的判断条件都变成了i < = j,和quicksort非常相似。因为排序的本质是数组划分。
因为在这里i和j要对撞之后错开才能保证所有的元素被审查过
public class Solution {
public int partitionArray(int[] nums, int k) {
if (nums == null || nums.length == 0) return 0;
int i = 0;
int j = nums.length - 1;
while (i <= j) {
while (i <= j && nums[i] < k) i++;
while (i <= j && nums[j] >= k) j--;
if (i <= j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
return j + 1;
}
}
Partition Array by Odd and Even
和上一道一样。
public class Solution {
public void partitionArray(int[] nums) {
if (nums == null || nums.length == 0) return;
int i = 0;
int j = nums.length - 1;
while (i <= j) {
while (i <= j && nums[i] % 2 == 1) i++;
while (i <= j && nums[j] % 2 == 0) j--;
if (i <= j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
}
}
Sort Letters by Case
二分都是一个意思,就当quicksort的复习。
public class Solution {
public void sortLetters(char[] chars) {
if(chars == null || chars.length == 0) return;
int i = 0;
int j = chars.length - 1;
while (i <= j) {
while (i <= j && Character.isLowerCase(chars[i])) i++;
while (i <= j && Character.isUpperCase(chars[j])) j--;
if (i <= j) {
char tmp = chars[i];
chars[i] = chars[j];
chars[j] = tmp;
}
}
}
}
三分
其实三分就是两个二分。
75. Sort Colors / Partition Array II
非常有名的算法,人称“荷兰旗算法” Dutch national flag problem,经典的 "3-way partitioning"算法,用于解决 quick sort 类排序算法中对于重复元素的健壮性问题,在原有 2-way partitioning 的基础上把所有 val == key 的元素集中于数组中间,实现【(小于),(等于),(大于)】的分区。
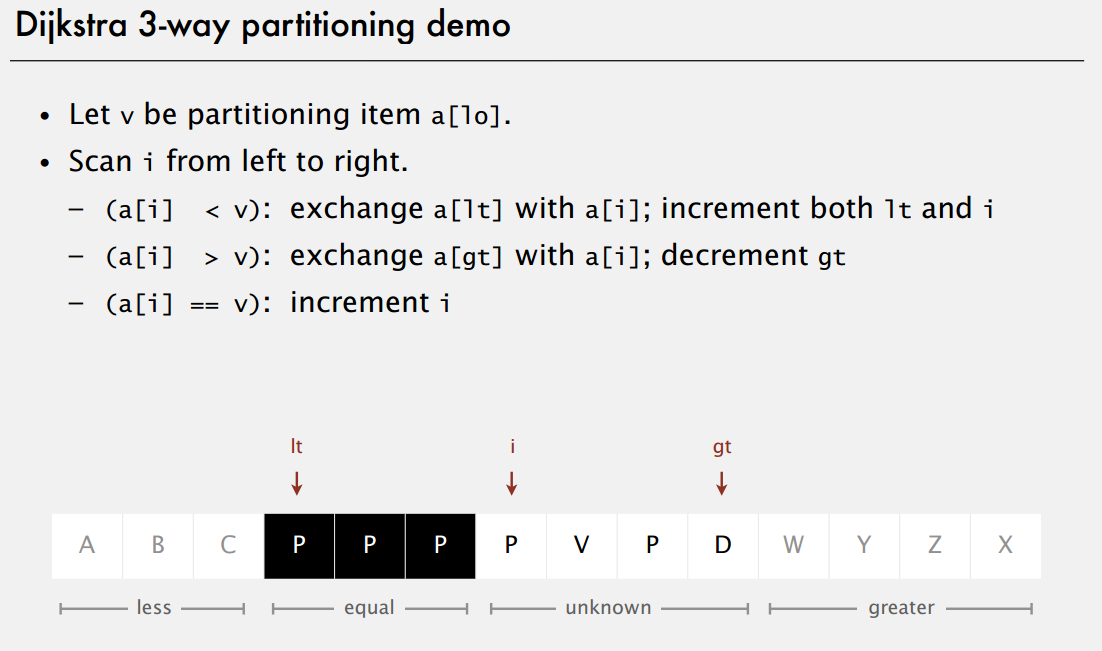
一张图说明 Dijkstra 的 3-way partitioning,左右指针维护 < key 和 > key 的元素,[left , cur - 1] 为 = key 的元素,[cur, right] 为未知元素。
只有在和 right 换元素时,cur 指针的位置是不动的,因为下一轮还要看一下换过来的元素是不是 < key 要放到左边。
O(n) 时间复杂度
public class Solution {
public void sortColors(int[] nums) {
if (nums == null || nums.length == 0) return;
int i = 0;
int left = 0;
int right = nums.length - 1;
while (i <= right) {
if (nums[i] == 0) {
swap(nums, left++, i++);
} else if (nums[i] == 2) {
swap(nums, i, right--);
} else i++;
}
}
private void swap(int[] nums, int a, int b){
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
Sort Colors II
进阶版,n个对象,k个颜色进行sort。
下面这个解法是延续自前面的思路,相当于每次排两个颜色,过去是可以AC的,现在TLE了,可以说lintcode的testcase也是越来越阴险了。
复杂度O(nk)
class Solution {
public void sortColors2(int[] colors, int k) {
int n = 0;
int start = 0;
int end = colors.length - 1;
while (n < k) {
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int j = start; j <= end; ++j) {
max = Math.max(max, colors[j]);
min = Math.min(min, colors[j]);
}
int i = start;
int left = start;
int right = end;
while (i <= right) {
if (colors[i] == min) {
swap(colors, left++, i++);
} else if (colors[i] == max) {
swap(colors, i, right--);
} else i++;
}
n += 2;
start = left;
end = right;
}
}
private void swap(int[] colors, int a, int b){
int tmp = colors[a];
colors[a] = colors[b];
colors[b] = tmp;
}
}
九章的解法,O(nlogk)的复杂度,把一个多分的问题转成递归二分的调用。
class Solution {
public void sortColors2(int[] colors, int k) {
if (colors == null || colors.length == 0) return;
rainbowSort(colors, 0, colors.length - 1, 1, k);
}
public void rainbowSort(int[] colors, int left, int right,
int colorFrom, int colorTo) {
if (colorFrom == colorTo) return;
if (left >= right) return;
int colorMid = (colorFrom + colorTo) / 2;
int l = left, r = right;
while (l <= r) {
while (l <= r && colors[l] <= colorMid) l++;
while (l <= r && colors[r] > colorMid) r--;
if (l <= r) {
int temp = colors[l];
colors[l] = colors[r];
colors[r] = temp;
l++;
r--;
}
}
rainbowSort(colors, left, r, colorFrom, colorMid);
rainbowSort(colors, l, right, colorMid + 1, colorTo);
}
}
还有一个特别好的解法,用的是桶排序的思想。
class Solution {
public void sortColors2(int[] colors, int k) {
if (colors == null) return;
int len = colors.length;
for (int i = 0; i < len; i++) {
// Means need to deal with A[i]
while (colors[i] > 0) {
int num = colors[i];
if (colors[num - 1] > 0) {
// 1. There is a number in the bucket,
// Store the number in the bucket in position i;
colors[i] = colors[num - 1];
colors[num - 1] = -1;
} else if (colors[num - 1] <= 0) {
// 2. Bucket is using or the bucket is empty.
colors[num - 1]--;
// delete the A[i];
colors[i] = 0;
}
}
}
int index = len - 1;
for (int i = k - 1; i >= 0; i--) {
int cnt = -colors[i];
// Empty number.
if (cnt == 0) {
continue;
}
while (cnt > 0) {
colors[index--] = i + 1;
cnt--;
}
}
}
}
215. Kth Largest Element in an Array
三分和二分的思路都可以做这个题,主要是递归调用去找区间,partition还是比较明显的。
public class Solution {
public int findKthLargest(int[] nums, int k) {
return partition(nums, k, 0, nums.length - 1);
}
private int partition(int[] nums, int k, int start, int end) {
int left = start;
int right = end;
int cur = start;
int pivot = nums[start];
while (cur <= right) {
if (nums[cur] > pivot) {
swap(nums, left++, cur++);
} else if (nums[cur] < pivot) {
swap(nums, cur, right--);
} else cur++;
}
if (k == right + 1) return nums[right];
if (k > right + 1) {
return partition(nums, k, right + 1, end);
} else return partition(nums, k, start, right - 1);
}
private void swap(int[] nums, int a, int b){
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
378. Kth Smallest Element in a Sorted Matrix
Nuts & Bolts Problem
所有的不等式判断条件都没有 '=' 号。
所有元素 1-1 对应,不会有多个元素等于 pivot.
pivot 元素来自外部,而不是内部已知位置。
如果 partition array 不带等于号的写,数组里有多个元素等于 pivot 就会挂了。 原因在于,在这题中,每次 partition 用的是外部元素,而且 array 里有且只有一个正确 pivot 元素与其对应,所以最终一定会 left == right 停留在 pivot 上。 这题如果像 partition 一样全带 '=' 去判断,其实也是可以正确把数组 partition 的,但是不同于 quick select 里面固定用 num[start] 做 pivot,这种写法里面我们不知道正确的 pivot 位置在哪。
假如按 left < = right,各种 cmp > = 0 < = 0 挪动
【2,1,|7|,8,3,9,|4|,5,6】,pivot = 5 【2,1,4,|8|,|3|,9,7,5,6】 【2,1,4,|3|,|8|,9,7,5,6】
总的来说
全带等号的比较方式,可以 partition,要手动找 pivot 位置做收尾 swap,适用于自己选好 pivot 的情况
全不带等号的比较方式,如果 pivot 元素有唯一对应,可以 partition 并且 left == right 停留在 pivot 上;否则多个等于 pivot 时会死循环,因为不带等号无法让指针跨过 等于 pivot 的元素。
/**
* public class NBCompare {
* public int cmp(String a, String b);
* }
* You can use compare.cmp(a, b) to compare nuts "a" and bolts "b",
* if "a" is bigger than "b", it will return 1, else if they are equal,
* it will return 0, else if "a" is smaller than "b", it will return -1.
* When "a" is not a nut or "b" is not a bolt, it will return 2, which is not valid.
*/
public class Solution {
public void sortNutsAndBolts(String[] nuts, String[] bolts, NBComparator compare) {
// write your code here
helper(nuts, bolts, compare, 0, nuts.length - 1);
}
private void helper(String[] nuts, String[] bolts, NBComparator compare,
int start, int end){
if(start >= end) return;
int pivot = partitionNuts(nuts, bolts[start], start, end, compare);
partitionBolts(bolts, nuts[pivot], start, end, compare);
helper(nuts, bolts, compare, start, pivot - 1);
helper(nuts, bolts, compare, pivot + 1, end);
}
private int partitionNuts(String[] nuts, String bolt, int start, int end,
NBComparator compare){
int left = start;
int right = end;
while(left < right){
while(left < right && compare.cmp(nuts[left], bolt) < 0) left ++;
while(left < right && compare.cmp(nuts[right], bolt) > 0) right --;
if(left < right) swap(nuts, left, right);
}
// 最终 left = right ,都停留在 pivot 上
return left;
}
private int partitionBolts(String[] bolts, String nut, int start, int end,
NBComparator compare){
int left = start;
int right = end;
while(left < right){
while(left < right && compare.cmp(nut, bolts[left]) > 0) left ++;
while(left < right && compare.cmp(nut, bolts[right]) < 0) right --;
if(left < right) swap(bolts, left, right);
}
return right;
}
private void swap(String[] arr, int a, int b){
String temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
};