前缀和,股票问题
美股不行,美股忙活一年还不如炒币一天的。Cryptocurrency人心浮躁啊。
121. Best Time to Buy and Sell Stock
买卖股票就是LC53 Maximum Subarray的变形,股票的涨跌幅度就是数组里面的正负数。
股票的涨跌:\,-6, 4,-2, 3,-2
股票的价格:7, 1, 5, 3, 6, 4 前缀和,原数组
这次给的原数组是前缀和,这下更省事了,不用维护前缀和数组,直接拿过来用就行了。
每次就计算当前价格减去历史价格中最小的就行,因为遍历顺序是天然从左至右的,所以根本不用担心先卖后买的错误,直接一个min维护最小值就行了,这个前缀和要比前面容易得多。开始的时候profit初始化为0是显而易见的。
public class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) return 0;
int max = 0;
int min = prices[0];
for (int i = 0; i < prices.length; ++i) {
max = Math.max(max, prices[i] - min);
min = Math.min(min, prices[i]);
}
return max;
}
}
122. Best Time to Buy and Sell Stock II
还是送分题,因为可以参与多次交易,只需要把每次的 increase 加在一起就可以了。
这里面min就变成了前一天的价格,因为可以无限次交易嘛,只要比前一天涨了,我们就有profit可以套,可惜现实世界没有预知未来这一说。
我觉得这种题还是多练练,要是面试问了写错了,那就太尬了。
public class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) return 0;
int max = 0;
int min = prices[0];
for (int i = 1; i < prices.length; ++i) {
if (prices[i] > min) {
max += prices[i] - min;
}
min = prices[i];
}
return max;
}
}
123. Best Time to Buy and Sell Stock III
在透彻理解了 Maximum Subarray II 之后,这道题完全就是个套了马甲的简化版。
k 次交易 = k 个 non-overlapping subarray
以这个角度去想,无非就是从两个方向扫描,利用 localMin / localMax 与当前元素的差值,去构造从左边/右边扫的 dp 数组。
left[i] : 从最左面到 i 所能获得的最大利益(单次交易)
right[i] : 从 i 到最右面所能获得的最大利益(单次交易)
然后拼起来就好了。要注意的细节:
每个位置并不是非交易不可,需要用 0 来代表不做交易的情况;
不是非要做 “两次交易” 不可,因此 left[end] 作为一次交易的代表,也要考虑在内。
public class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) return 0;
int n = prices.length;
int[] left = new int[n];
int[] right = new int[n];
int profit = 0;
int min = prices[0];
left[0] = 0;
for (int i = 1; i < n; ++i) {
profit = Math.max(profit, prices[i] - min);
min = Math.min(min, prices[i]);
left[i] = profit;
}
profit = 0;
int max = prices[n - 1];
right[n - 1] = 0;
for (int i = n - 2; i >= 0; --i) {
profit = Math.max(profit, max - prices[i]);
max = Math.max(max, prices[i]);
right[i] = profit;
}
int twoTran = 0;
for (int i = 0; i < n - 1; ++i) {
twoTran = Math.max(twoTran, left[i] + right[i + 1]);
}
int leftTran = 0;
int rightTran = 0;
for (int i = 0; i < n; ++i) {
leftTran = Math.max(leftTran, left[i]);
rightTran = Math.max(rightTran, right[i]);
}
return Math.max(twoTran, Math.max(leftTran, rightTran));
}
}
不是非要做 “两次交易” 不可,因此 left[end] 作为一次交易的代表,也要考虑在内。
所以最后那段代码完全可以改为:
int result = 0;
for(int i = 0; i < n - 1; i++){
result = Math.max(result, left[i] + right[i + 1]);
}
// might be completely on left side;
result = Math.max(result, left[n - 1]);
return result;
188. Best Time to Buy and Sell Stock IV
延续了 Maximum Subarray III 的优良传统。
309. Best Time to Buy and Sell Stock with Cooldown
第一反应这不就是T + 1交易变形。。。
友情提示:这题是@dietpepsi加的。
继承了原来股票问题的思路和 local 结构: 必须在第 i 天卖。 现在多了一种新操作"You do nothing",就需要定义一个新数组。
考虑到股票 diff 的可拼接性质,sell[i] 可以直接由 sell[i - 1] + diff 构造而成;同时也可以由 do_nothing[i - 2] + diff 构造成,代表着上一次 sell 操作发生在 i - 3 事,i - 2 do_nothing, i - 1 买入, i 卖出的情形。
由这题我们可以发现,实际需要的 dp[] 数量是取决于操作数量的,要以“用当前操作结尾”来定义 localMax. 只不过在之前的问题中,因为买入卖出可以拼接,我们略去了 buy 的数组。
这题扩展开来的话,也可以扩展到 cooldown k 天,所依赖的状态,初始化,循环的起始位置会有变化而已。
前缀和问题我总犯一个错误,总是把i和n写混,小bug很烦。
public class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length <= 1) return 0;
int n = prices.length;
int[] sell = new int[n];
int[] cool = new int[n];
sell[1] = prices[1] - prices[0];
for (int i = 2; i < n; ++i) {
cool[i] = Math.max(cool[i - 1], sell[i - 1]);
sell[i] = Math.max(sell[i - 1], cool[i - 2]) + prices[i] - prices[i - 1];
}
return Math.max(sell[n - 1], cool[n - 1]);
}
}
居然有人用状态机去写这类题,好巧妙啊。就是图画得有点丑。
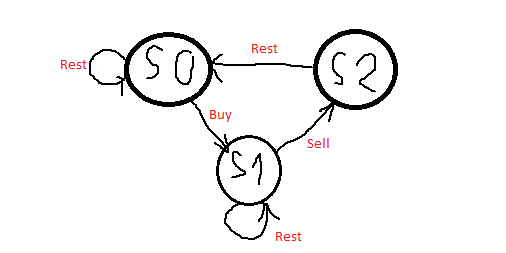
https://leetcode.com/discuss/72030/share-my-dp-solution-by-state-machine-thinking
在整个交易过程中,我们只可能处于如上图所示的三种状态中。
这个解法的要点是,每个 state 的 in-degree 代表能到达当前 state 的所有可能操作。
s0 可能由上一次的 s0,或上一次的 s2 卖掉而来;
s1 可能由上一次的 s1,或者上一次的 s0 买入而来;
s2 只可能由 s1 的卖出而来。
public class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
if (n <= 1) return 0;
int[] s0 = new int[n];
int[] s1 = new int[n];
int[] s2 = new int[n];
s0[0] = 0;
s1[0] = -prices[0];
s2[0] = Integer.MIN_VALUE;
for (int i = 1; i < n; i++) {
s0[i] = Math.max(s0[i - 1], s2[i - 1]);
s1[i] = Math.max(s1[i - 1], s0[i - 1] - prices[i]);
s2[i] = s1[i - 1] + prices[i];
}
return Math.max(s0[n - 1], s2[n - 1]);
}
}