双序列型动态规划

双序列顾名思义就是俩单序列放一块问你怎么做。这个章节的题都比较难，跳过也行。

• state: f[i][j]代表了第一个sequence的前i个数字/字符，配上第二个sequence的前j个...

• function: f[i][j] = 研究第i个和第j个的匹配关系

• initialize: f[i][0] 和 f[0][i]

• answer: f[n][m]

• n = s1.length()，m = s2.length()

Longest Common Subsequence

问题定义

应该是LC14 Longest Common Prefix的升级版，很奇怪为什么leetcode没有这道题，我现在对LC越来越疑惑了，加了那么多乱七八糟的题，一些经典题目都没有，像是背包问题都没有。

两个字符串的最后两个字符i和j，如果match，那么这时一定是最长的，+1。

如果不match，两种情况

• A[i]不能和任何match，f[i - 1][j]
• A[j]不能和任何match，f[i][j - 1]

选一个比较长的。A[i][j]都不能match的情况是最短的，已经包含在f[i - 1][j - 1]内了。

public class Solution {
    public int longestCommonSubsequence(String A, String B) {
        if (A == null || B == null || A.length() == 0 || B.length() == 0) return 0;

        int m = A.length();
        int n = B.length();
        int[][] f = new int[m + 1][n + 1];

        for (int i = 0; i <= m; ++i) {
            f[i][0] = 0;
        }
        for (int i = 0; i <= n; ++i) {
            f[0][i] = 0;
        }
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
                if(A.charAt(i - 1) == B.charAt(j - 1)) {
                    f[i][j] = f[i - 1][j - 1] + 1;
                }
            }
        }
        return f[m][n];
    }
}

提一下算法导论这道题的优化方式。

给定长度为 m 的字符串 {1,2,3...m} ，其 subsequences 的数量总数为 2^m，即对每个字符选择 “取 / 不取”。

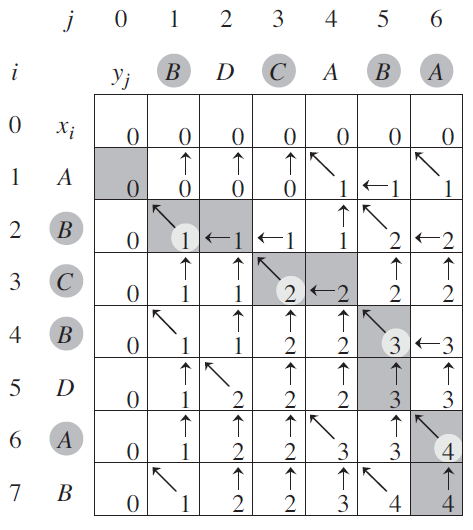
于是有了下面的可视化版本

这个版本的做法非常适合存储和输出 optimal path，也可以应用到 Longest Increasing Subsequence 中，用于 follow-up 情况下输出 sequence.

比如输入数组为 X = [x1, x2 .. xn]，其排序后的数组为 X' = [x'1, x'2 .. x'n]

• LIS 即 X 与 X' 的 LCS，判断条件完全一样，元素相等向右下走。如果每一步上都存行进方向，那么最后从右下角往左上出发，每一步指向左上角的箭头都是 LIS 的元素。

滚动数组优化版的代码，最大值肯定在 dp[][] 的最右下角。

public class Solution {
    public int longestCommonSubsequence(String A, String B) {
        if(A == null || B == null) return 0;

        int n = A.length();
        int m = B.length();
        if(n == 0 || m == 0) return 0;

        int[][] dp = new int[2][m + 1];

        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(A.charAt(i - 1) == B.charAt(j - 1)){
                    dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1; 
                } else {
                    dp[i % 2][j] = Math.max(dp[(i - 1) % 2][j], dp[i % 2][j - 1]); 
                }

            }
        }
        return dp[n % 2][m];
    }
}

72. Edit Distance

Hard题。关于这个问题最好的 slides, by Stanford

这道题和LCS很像，求的是最小。可以很容易看到只依靠 LCS 长度解决这道题的乏力；因为 LCS 长度和 edit distance 对字符串结构的利用是不一样的，mismatch 的字符可以出现错位，而 edit distance 不支持一次操作进行修正。算法导论上也写的非常清楚，鉴定两条 DNA 序列的相似度，substring 是一种思路（KMP），LCS是一种思路，而 edit distance 是另一种思路。

三种操作，插入，删除，替换，word1变成word2。

• state: f[i][j] 表示A的前 i 个字符最少几次操作变成 B 的前 j 个字符。

定义结束后，我们来分析一下转移方程的可能性。

• 如果 A 的第 i 个字符等于 B 的第 j 个字符，换句话说就是当前位的字母相同了，这是我们最喜欢的结果，因为不用操作就相同了。这时我们有三种选择：

  • 首先，我们可能不需要第 i 个字符，问题变成了用最少的操作把前 i - 1 个字符变为前 j 个字符。也就是删除：f[i - 1][j] + 1
  • 其次，可能不删掉第 i 个字符，而是在后面加一个字符，一次操作使 A 的前 i 个字符与 B 的前 j - 1 个字符相等：f[i][j - 1] + 1
  • 在 i，j 相同的情况下也可能不需要新的操作，f[i - 1][j - 1]

• 如果 A 的第 i 个字符 不等于 B 的第 j 个字符：

  • 很简单，我们需要一次replace操作：f[i - 1][j - 1] + 1

• function:

  • f[i][j] = MIN(f[i - 1][j] + 1, f[i][j - 1] + 1, f[i - 1][j - 1]) // A[i - 1] == B[j - 1]
  • MIN(f[i - 1][j] + 1, f[i][j - 1] + 1, f[i - 1][j - 1] + 1) // A[i - 1] != B[j - 1]
• initialize: f[i][0] = i, f[0][j] = j
• answer: f[m][n]

public class Solution {
    public int minDistance(String word1, String word2) {
        if (word1 == null && word2 == null || word1.length() == 0 && word2.length() == 0) return 0;
        int m = word1.length();
        int n = word2.length();

        int[][] f = new int[m + 1][n + 1];

        for (int i = 0; i <= m; ++i) {
            f[i][0] = i;
        }
        for (int i = 0; i <= n; ++i) {
            f[0][i] = i;
        }

        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    f[i][j] = Math.min(Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1), f[i - 1][j - 1]);
                } else {
                    f[i][j] = Math.min(Math.min(f[i - 1][j] + 1, f[i][j - 1] + 1), f[i - 1][j - 1] + 1);
                }
            }
        }
        return f[m][n];
    }
}

这题花了我很久的时间才理解和AC，如果做不出来我觉得没关系，Hard题不是我们的主要目标，没有多少公司会一直考你Hard题目，那样怎么会有区分度呢？

这道题让我觉得是时候结束DP的题目了，纠缠在难题上面是对一种精力消耗和时间浪费。

Minimum insertions to form a palindrome

和 Edit distance 非常像，考虑到 add/delete 在构造 string 上的等价性质，问题的 optimal substructure 即为

f[i][j] = substring(i,j) 范围内，构造 palindrome 的最小编辑次数

• 如果 s[i] == s[j]

  • f[i][j] = f[i + 1][j - 1] (不需要操作)

  • 同时考虑 i , j 相邻的情况

• 如果 s[i] != s[j]，那么我们可以经 add/delete 操作构造出当前的 s(i, j)

  • s(i + 1, j) + ADD

  • s(i, j - 1) + ADD

注意这题不支持 replace，如果支持的话，f[i][j] 还要看一个新状态，f[i + 1][j - 1]

public class Main {
    private static int minEditDistance(String str){
        if (str == null || str.length() <= 1) return 0;

        int n = str.length();

        // f[i, j] = min edit distance for substring (i, j);
        int[][] f = new int[n][n];
        for (int i = 1; i < n; ++i) {
            for (int j = i; j >= 0; --j) {
                if (j == i) {
                    f[j][i] = f[i][j] = 0;
                } else {
                    if (str.charAt(i) == str.charAt(j)) {
                        f[j][i] = f[i][j] = (j + 1 == i) ? 0
                                : f[j + 1][i - 1];
                    } else {
                        f[j][i] = f[i][j] = (j + 1 == i) ? 1
                                : Math.min(f[j + 1][i], f[j][i - 1]) + 1;
                    }
                }
            }
        }
        return f[0][n - 1];
    }
}

115. Distinct Subsequences

求方案总数的一道双序列题。Hard题。

S = "rabbbit", T = "rabbit" Return 3

rab1b2b3it，S 里面有三个b，T 里面有两个 b，也就是两个b去匹配三个b有多少种方案，显然是三种，我们可以选择b1b2，b1b3，b2b3. 注意顺序要对（显然）。

再举个例子，rrabbbit 和 rabbit，这时我们有2 * 3 = 6种方案。

像是上一道题，但这次你不能把 T 里面的字符扔掉，只能扔 S。双序列的动态规划记住总是去匹配最后一个字符是否相等。

如果是求最大/小，60-70% 是动态规划。 如果是求方案总数，99% 是动态规划。当然你用DFS也可以，如果不会栈溢出的话。

• state: f[i][j] 表示 S 的前 i 个字符中选取 T 的前 j 个字符，有多少种方案
• function:
  • 如果最后一个字符 相等：f[i][j] = f[i - 1][j] + f[i - 1][j - 1] // S[i - 1] == T[j - 1]
  • 如果最后一个字符 不相等：f[i][j] = f[i - 1][j] // S[i - 1] != T[j - 1]
• initialize: f[i][0] = 1, f[0][j] = 0 (j > 0)
• answer: f[m][n] (m = sizeof(S), n = sizeof(T))

public class Solution {
    public int numDistinct(String s, String t) {
        if (s == null && t == null || s.length() == 0 && t.length() == 0) return 0;

        int m = s.length();
        int n = t.length();
        int[][] f = new int[m + 1][n + 1];

        for (int i = 0; i <= m; ++i) {
            f[i][0] = 1;
        }
        for (int i = 1; i <= n; ++i) {
            f[0][i] = 0;
        }

        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
                } else {
                    f[i][j] = f[i - 1][j];
                }
            }
        }
        return f[m][n];
    }
}

97. Interleaving String

Hard题。但相比于前面已经容易一些了。

三个string，s1，s2，s3，s3能不能被s1和s2交替组成，判断是否可行的一道题。

有点merge sorted array的感觉。

首先从题目结构来看，和这章的前几道双序列 DP 非常相似，都是一个字符串 “构造问题”，即用小的 substring 通过生长和拼接，构造出更大的目标 string. 一般这类问题有天然的 bottom-up 思路，当然，top-bottom 的递归思路也是完全可行的。

f[i][j][k] 表示 s1 的前 i 个字符和 s2 的前 j 个字符能否交替组成 s3 的前 k 个字符，但是这里面 k = i + j，这时肯定的，所以一个三维的数组没什么意义。

同时我们也要处理好 i = 0 和 j = 0 的初始化条件。

时间空间复杂度 O(s1.len * s2.len)

• state: f[i][j]表示 s1 的前 i 个字符和 s2 的前 j 个字符能否交替组成 s3 的前 i + j 个字符
• function:
  • f[i][j] = (f[i - 1][j] && (s1[i - 1] == s3[i + j - 1]) ||
  • f[i][j] = (f[i][j - 1] && (s2[j - 1] == s3[i + j - 1])
• initialize:
  • f[i][0] = (s1[0..i - 1] == s3[0..i - 1])
  • f[0][j] = (s2[0..j - 1] == s3[0..j - 1])
• answer: f[m][n], m = sizeof(s1), n = sizeof(s2)

public class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        if(s1 == null || s2 == null || s3 == null) return false;
        if(s3.length() != s1.length() + s2.length()) return false;
        if(s1.length() == 0) return s2.equals(s3);
        if(s2.length() == 0) return s1.equals(s3);

        int m = s1.length();
        int n = s2.length();

        boolean[][] f = new boolean[m + 1][n + 1];

        f[0][0] = true;
        for (int i = 1; i <= m; ++i) {
            f[i][0] = (s1.charAt(i - 1) == s3.charAt(i - 1)) && f[i - 1][0];
        }
        for (int i = 1; i <= n; ++i) {
            f[0][i] = (s2.charAt(i - 1) == s3.charAt(i - 1)) && f[0][i - 1];
        }

        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                f[i][j] = (f[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)) ||
                            (f[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));
            }
        }
        return f[m][n];
    }
}

10. Regular Expression Matching

44. Wildcard Matching

public class Solution {
    public boolean isMatch(String s, String p) {
        if(s == null || p == null) return false;
        int m = s.length();
        int n = p.length();
        boolean[][] f = new boolean[m + 1][n + 1];

        f[0][0] = true;

        for (int i = 1; i <= n; ++i) {
            if (p.charAt(i - 1) == '*') f[0][i] = true;
            else break;
        }

        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                char chs = s.charAt(i - 1);
                char chp = p.charAt(j - 1);
                if (chp != '*' && chp != '?') {
                    f[i][j] = f[i - 1][j - 1] && chs == chp;
                } else if (chp == '?') {
                    f[i][j] = f[i - 1][j - 1];
                } else if (chp == '*') {
                    f[i][j] = f[i - 1][j] || f[i][j - 1] || f[i - 1][j - 1];
                }
            }
        }
        return f[m][n];
    }
}