区间类DP
DP做的我烦躁啊。
求一段区间的解 min/max/count
相比划分类 DP ,区间类 DP 为连续相连的 subproblem ,中间不留空,更有 divide & conquer 的味道。
转移方程通过区间更新
从大到小的更新
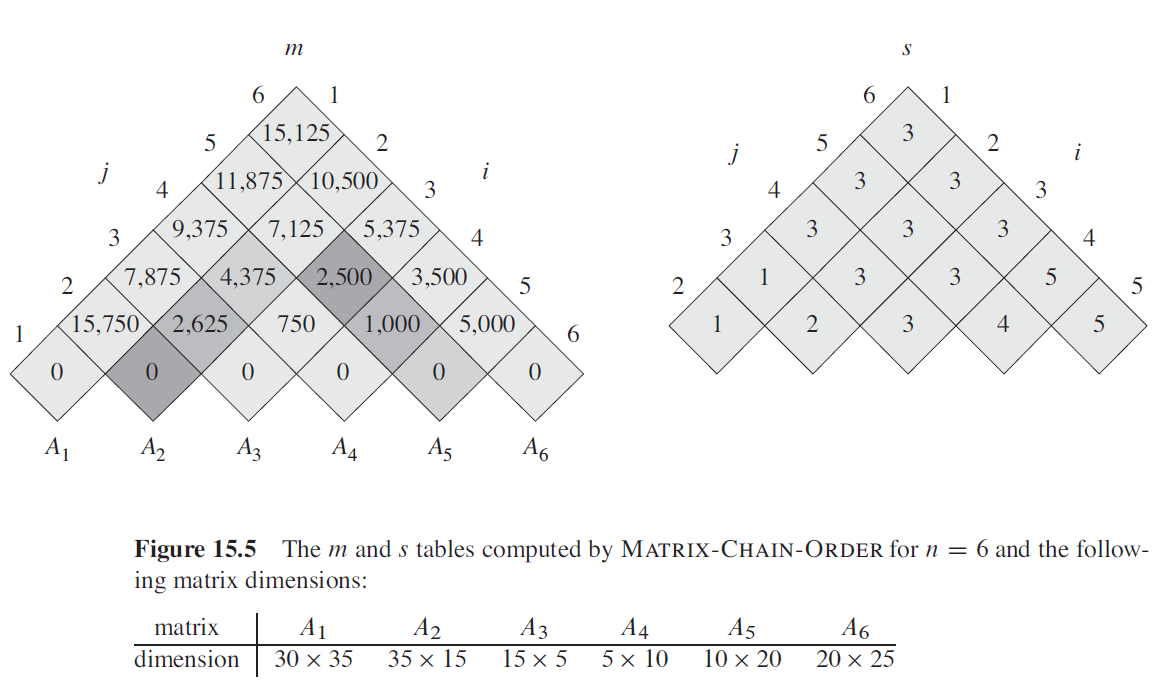
Matrix-chain multiplication (算法导论)
给定矩阵向量 [A1, A2, A3 .. An]
矩阵乘法有结合律,所以任意的 parenthesization 结果一样
Dimension (a x b) 乘 (b x c) 得到 (a x c) ,总计算量为 a x b x c
可能的括号加法为 Catalan 数,O(2^n),因而搜索不合适。

让 dp[i][j] 代表(i , j) 区间内最优的括号顺序运算次数
符合 optimal substructure,反证法
A = rows * cols,假如从 k 分开左右 i <= k < j ,如下 k = 5 时:
[A1, A2, A3, A4, A5 || A6, A7,A8,A9]
左子问题为 A1.rows x A5.cols
右子问题为 A6.rows x A9.cols
其中 A5.cols = A6.rows
其总花费为 dp[1,5] + dp[6,9] + A1.rows A5.cols A9.cols
至此,对于任意 size (i , j) 的向量区间,我们都可以遍历所有合理 k 的切分点,实现记忆化的 divide & conquer,当前区间的最优解一定由其最优子区间拼接而成。

子问题图如下。其实就是一个 n x n 的矩阵对角线,代表所有的子区间。
132. Palindrome Partitioning II
上一题的求所有区间最优解进行拼接的思路和 optimal substructure 结构和这题非常像,再贴一遍,感受一下。
不过 Matrix Chain Multiplication 要比这个复杂,时间复杂度为 O(n^3). 毕竟每个切点上会生成两个 subproblems.
public class Solution {
public int minCut(String s) {
if(s == null || s.length() <= 1) return 0;
int len = s.length();
boolean[][] isPalindrome = new boolean[len][len];
int[] dp = new int[len];
for(int i = 0; i < len; i++){
dp[i] = i;
for(int j = 0; j <= i; j++){
if(s.charAt(i) == s.charAt(j) && (i - j < 2 || isPalindrome[j + 1][i - 1])){
isPalindrome[i][j] = isPalindrome[j][i] = true;
if(j == 0){
dp[i] = 0;
} else {
dp[i] = Math.min(dp[i], dp[j - 1] + 1);
}
}
}
}
return dp[len - 1];
}
}
Valid Palindrome
- State: f[i][j]表示index从i到j这一段是不是一个回文串
- Function: f[i][j] = f[i + 1][j - 1] && (s[i] == s[j])
- Initialize: f[i][i] = true
- Answer: f[x][y] // x, y是你想查询的那一段区间
注意不要越界,注意初始化。
i 依赖于i + 1,算的时候要倒过来,先算大的。本质上是先for区间长度,再for左端点。
这个valid解法和LC125 Valid Palindrome不一样,因为LC125要忽略空格和符号。这个解法其实实战并没有什么优势,只是区间型动态规划的一个例子。
public class Solution {
public boolean isPalindrome(String s) {
if (s == null || s.length() == 0) return true;
int n = s.length();
boolean[][] f = new boolean[n][n];
for (int i = 0; i < n; ++i) {
f[i][i] = true;
}
for (int i = 0; i < n - 1; ++i) {
f[i][i + 1] = (s.charAt(i) == s.charAt(i + 1));
}
for (int i = n - 1; i >= 0; --i) {
for (int j = i + 2; j < n; ++j) {
f[i][j] = f[i + 1][j - 1] && s.charAt(i) == s.charAt(j);
}
}
return f[0][n - 1];
}
}