图的基本性质和操作
Graph 是非常重要而又涵盖很广的内容,以至于有单独的 “图论” 研究方向。LeetCode 上很多问题都可以抽象成 “图” ,比如搜索类问题,树类问题,迷宫问题,矩阵路径问题,等等。
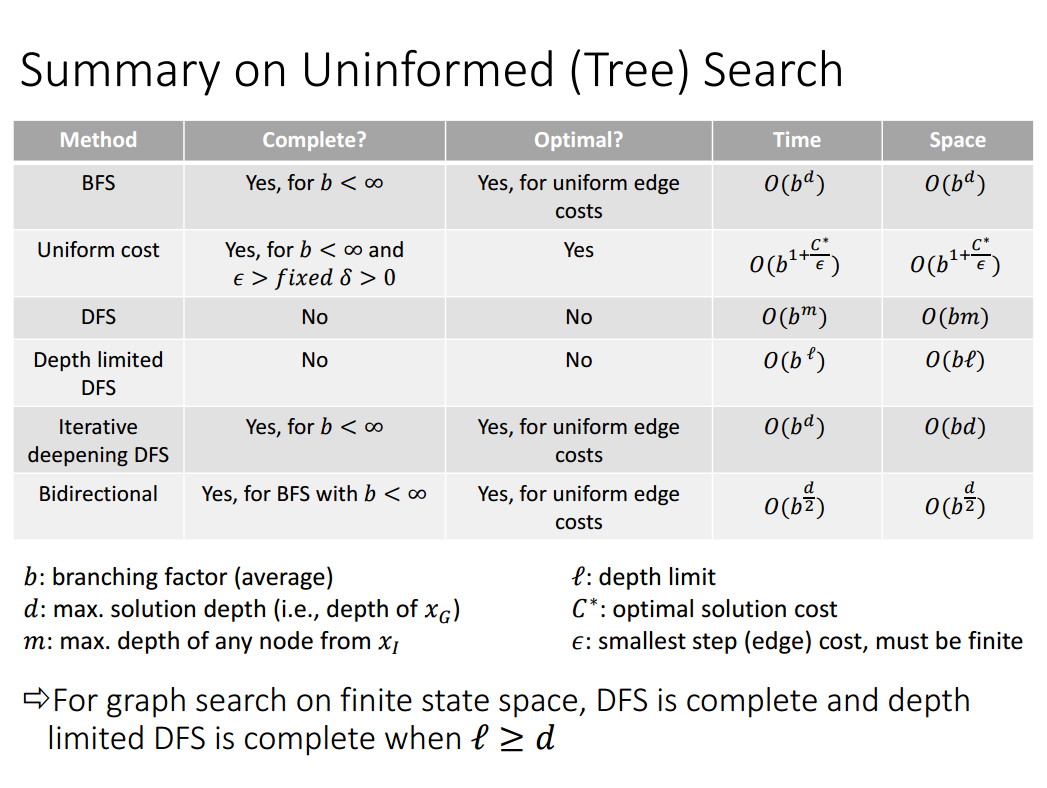
BFS 的时间空间占用以 branching factor 为底, 到解的距离 d 为指数增长;空间占用上 Queue 是不会像 DFS 一样只存一条路径的,而是从起点出发越扩越大,因此会有空间不够的风险,空间占用为 O(b^d)。
DFS 的时间占用以 branching factor 为底,树的深度 m 为指数增长;而空间占用上,却只是 O(bm),可视化探索过程中只把每个 Node 的所有子节点存在 Stack 上, 探索完了再 pop 出来接着探,因此储存的节点数为 O(bm)。
可以看到无论是 BFS 还是 DFS,树的 branching factor 都是对空间与时间复杂度影响最大的参数;除此之外,BFS 中最重要的是到解的距离,而 DFS 看从当前节点的深度。普遍来讲,DFS 空间上会经济一些,当然也要分情况讨论。
Topological sort,拓扑排序,是 graph 搜索中一种特殊的顺序,本质上还是完全可以靠 BFS / DFS 解决。
有向图 DFS 图示:
有向图 BFS 图示:
有向图 Directed:
DFS:
Detect Cycle (Course Schedule)
暴力解法:DFS + Backtracking,寻找“所有从当前节点的” path,如果试图访问 visited 则有环;缺点是,同一个点会被探索多次,而且要从所有点作为起点保证算法正确性,时间复杂度非常高
最优解法是 CLRS 上用三种状态表示每个节点:
- "0" 还未访问过;
- "1" 代表正在访问;
- "2" 代表已经访问过;
DFS 开始时把当前节点设为 "1";
在从任意节点出发的时候,如果我们试图访问一个状态为 "1" 的节点,都说明图上有环。
当前节点的 DFS 结束时,设为 "2";
在找环上,DFS 比起 BFS 最大的优点是"对路径有记忆",DFS 记得来时的路径和导致环的位置,BFS 却不行。
Topological Sort
类似剥洋葱,可以选择任意点开始向里 DFS ,记录path,后面做的其他 DFS path 都放在之前结果的前面。(CLRS有)
等价做法是,把每次 DFS 探索中的 path 按照由内向外的顺序添加(单序列反序), 后进行的 DFS 结果放在之前运行完的结果后面(全序列反序),然后 reverse 就好了,可以改良 ArrayList 添加的时间复杂度。
更简单的做法是用 Java 内置的 LinkedList,支持双端操作。
Count # of connected components
Determine if A is reachable from B
BFS:
Detect Cycle (Course Schedule)
首先,在 DAG 上找环,DFS 要比 BFS 强。
其次重点注意,有向图靠 3 个状态 BFS 是不能正确判断是否有环的,要靠 indegree,一个例子是 【0, 1】 和 【1,0】,环在发现之前已经被标注为 state 2 了。
扫一遍所有 edge,记录每个节点的 indegree.
在有向无环图中,一定会存在至少一个 indegree 为 0 的起点,将所有这样的点加入queue。
依次处理queue里的节点,把每次poll出来的节点的 children indegree -1. 减完之后如果 child 的 indegree = 0 了,就也放入队列。
如果图真的没有环,可以顺利访问完所有节点,如果还有剩的,说明图中有环,因为环上节点的 indegree 没法归 0.
Topological Sort
步骤同上,扫的时候按顺序 append 就好了。
类似于“剥洋葱”,从最外面一层出发,逐步向里。
Count # of connected components
Determine if A is reachable from B
这个任务最适合用 BFS 做,从 B 做起点一路扫看看能不能扫到 A 就行了。
无向图 Undirected:
无向图算法的整体思路和有向图基本一致,但是需要重点注意 正确处理 “原路返回” 的情况,免得死循环或者误报。
在无向图的2个状态基础上增加一个 “正在访问” 的新状态,加上注意 prev 就可以了。
DFS:
Detect Cycle (Graph Valid Tree)
用 int[] 表示每个点的状态,其中
- 0 代表“未访问”;
- 1 代表“访问中”;
- 2 代表“已访问”;
DFS call 里要传入 "prev节点" 参数,避免出现原路返回,或者回到前一个节点误判为有环。(和 directed graph DFS 唯一的不同之处)
其他情况下,如果我们试图访问一个状态为 “1” 的节点,都可以说明图中有环。
Count # of connected components (Graph Valid Tree)
Determine if A is reachable from B
BFS:
Detect Cycle (Graph Valid Tree)
扫描所有 edges 记录图到底长啥样;
用 "0,1,2" states;
随便扔一个点进 queue,标记 "1",然后 BFS,所有 child = "0" 的都加入队列
所有 child 都检查完之后,立刻把当前 node = 2,不然下一层 BFS 会回头去看自己然后误报。
如果遇到 child = "1" 的说明有环
Count # of connected components (Graph Valid Tree)
和 Detect Cycle 一样,同时记录下到底做了几次 BFS 才扫遍全图,图上就有几个 connected components
Determine if A is reachable from B
BFS 搜到底看看能不能到就可以了,这个和只靠 g(x) 的 uniform-cost search 一致。