跟Integer相关的12,13,38,273我放在后面了。
2. Add Two Numbers
链表的时候我们写过一道题是这样的。回忆一下,然后看下一道题。
public class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
int carry = 0;
ListNode dummy = new ListNode(0);
ListNode node = dummy;
while (l1 != null && l2 != null) {
int sum = l1.val + l2.val + carry;
node.next = new ListNode(sum % 10);
carry = sum / 10;
l1 = l1.next;
l2 = l2.next;
node = node.next;
}
while (l1 != null) {
int sum = l1.val + carry;
node.next = new ListNode(sum % 10);
carry = sum / 10;
l1 = l1.next;
node = node.next;
}
while (l2 != null) {
int sum = l2.val + carry;
node.next = new ListNode(sum % 10);
carry = sum / 10;
l2 = l2.next;
node = node.next;
}
if (carry != 0) {
node.next = new ListNode(carry);
node = node.next;
node.next = null;
}
return dummy.next;
}
}
67. Add Binary
上题完全一样的思路应用在二进制计算上就行了。十进制和二进制区别也就是%取余时用10和2。进位操作也是完全相同的。
这道题不同的是,当问题非常简单的时候,解题重点就从优化时间复杂度变成了优化代码简洁性。
这题代码简洁的重点在于处理“终止条件”,因为两个 string 很可能长度不一,也有可能两个 string 加完了之后还有进位没处理。
输入长短不一就都放在 while loop 里,在读取字符时把短的做 padding
While loop 里三个 'OR' 的条件保证了三种不同情况下都会继续读取,而其他两个自动 pad 0
public class Solution {
public String addBinary(String a, String b) {
StringBuilder sb = new StringBuilder();
int i = a.length() - 1;
int j = b.length() - 1;
int carry = 0;
while (i >= 0 || j >= 0 || carry == 1) {
int digitA = i < 0 ? 0 : a.charAt(i--) - '0';
int digitB = j < 0 ? 0 : b.charAt(j--) - '0';
sb.append((digitA + digitB + carry) % 2);
carry = (digitA + digitB + carry) / 2;
}
return sb.reverse().toString();
}
}
43. Multiply Strings
又进阶了,这次是乘法,比加法复杂。
下面的解法是九章算法的,简洁高效。非常聪明巧妙。
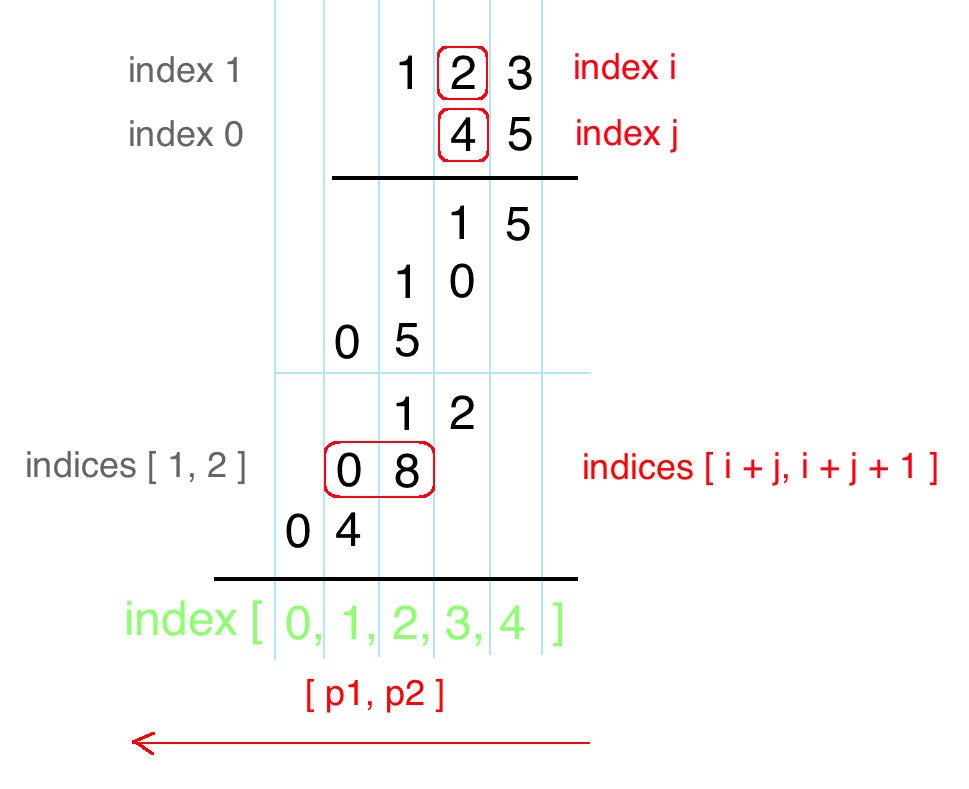
两个位数为 m 和 n 的数字相乘,乘积不会超过 m + n 位。
乘法操作从右往左计算时,每次完成相加就确定了当前 digit.
同一个 digit 多次修改,用 int[]
进位的trick都是一样的。注意最后的index和maxLength,利用长度和下标,简单的规避了任何一个数字为0的corner case,非常的简洁。
public class Solution {
public String multiply(String num1, String num2) {
if (num1 == null || num2 == null) return null;
int maxLength = num1.length() + num2.length();
int[] result = new int[maxLength];
for (int i = num1.length() - 1; i >= 0; --i) {
int j, carry = 0;
for (j = num2.length() - 1; j >= 0; --j) {
int digit1 = num1.charAt(i) - '0';
int digit2 = num2.charAt(j) - '0';
int product = digit1 * digit2 + carry + result[i + j + 1];
result[i + j + 1] = product % 10;
carry = product / 10;
}
result[i + j + 1] = carry;
}
StringBuilder sb = new StringBuilder();
int index = 0;
while (index < maxLength - 1 && result[index] == 0) index++;
while (index < maxLength) sb.append(result[index++]);
return sb.toString();
}
}