Morris 遍历

看这个

1968年，Knuth提出说能否将该问题的空间复杂度压缩到O(1)，同时原树的结构不能改变。大约十年后，1979年，Morris在《Traversing Binary Trees Simply and Cheaply》这篇论文中用一种Threaded Binary Tree的方法解决了该问题。

Morris算法在遍历过程中动态的构建Threaded Binary Tree，同时在结束时又将树恢复原样，在满足O(1)空间复杂度的同时也恰好满足Knuth对树结构不能改变的要求。

preorder/inorder遍历：每次访问root左子树之前，先找到左子树里面最右面的点，并把其 right 指针连到 root 上；左子树遍历完这个点之后，再把这个多出来的指针拆掉。

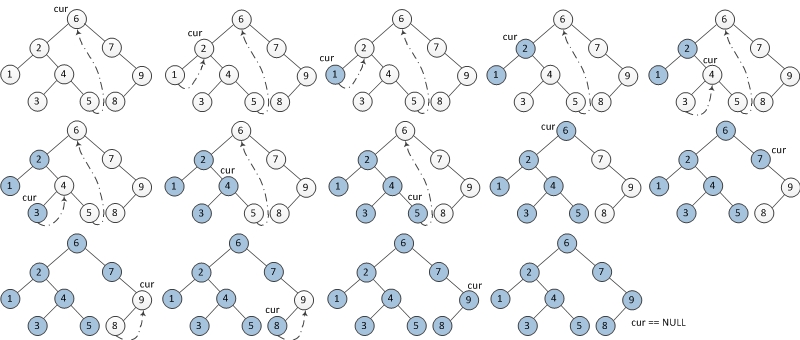
if(prev.right == null){
    ...
} else {
    ...
}

既是建立threaded节点也是拆除节点的地方。prev.right可能为空（未建立指针），也可能不为空（已建立指针，指针指向下一个遍历节点）。

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<Integer>();
        TreeNode cur = root;
        while(cur != null){
            if(cur.left == null){
                list.add(cur.val);
                cur = cur.right;
            } else {
                TreeNode prev = cur.left;
                while(prev.right != null && prev.right != cur){
                    prev = prev.right;
                }
                if(prev.right == null){
                    prev.right = cur;
                    // Uncomment for pre-order
                    // list.add(cur.val);
                    cur = cur.left;
                } else {
                    prev.right = null;
                    // Uncomment for in-order
                    // list.add(cur.val);
                    cur = cur.right;
                }
            }
        }
        return list;
    }
}

postorder遍历

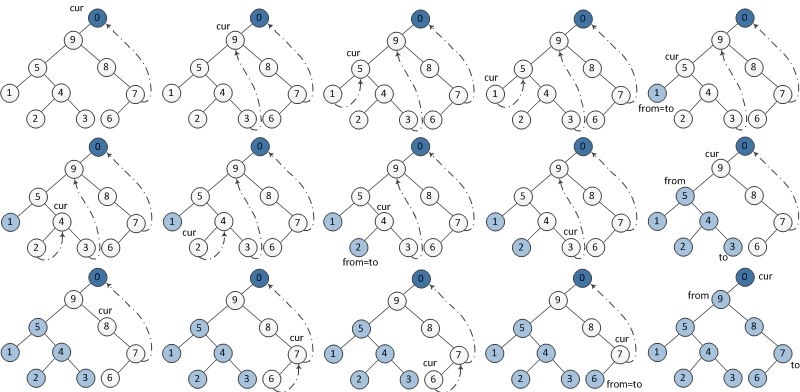
算法思想与前序和中序遍历一致，只不过我们需要添加一个新的根节点，这个新的根节点的左子树为原树的根节点，右子树为空。假设当前节点为cur，在遍历完了cur.left的左子树以后，我们逆向遍历从cur.left到cur的中序遍历前驱节点间的所有节点，这样就可以实现cur的左子树的后序遍历。因为最开始我们添加了一个新的根节点，它的左子树是原树，所以可以保证最终我们能够得到整个树的后序遍历。

postorder的Morris遍历要建一个dummy node以及反序输出，个人感觉并不是很practical。复习时再回头仔细研究吧。

时间复杂度

表面上看我们的程序中包含有两层的while循环，但实际上Morris算法的时间复杂度仍然是O(n)。对于前序和中序遍历，假设有n个节点，二叉树中的n-1条边每条边最多被访问2次。第一次是确定当前节点的前驱节点，第二次是从前驱节点返回到当前节点以后的再次访问。所以总体上来看，算法复杂度是O(2n)=O(n)。

对于后序遍历，因为比前序和中序遍历多了两次反转操作(reverse)，这就导致每条边最多被访问4次，最终算法复杂度是O(4n)=O(n)。

Morris算法虽然在时间复杂度上有着系数级别的差异，但却带来了空间复杂度量级上的降低。总体看来，在某些空间苛刻的场景中，该算法非常实用。

99. Recover Binary Search Tree

这道题是BST，很明显用Morris的中序遍历可以实现真正的 O(n) 时间 O(1) 空间。

(prevNode != null && prevNode.val >= cur.val) 为真时：

p == null：说明prev指向第一个错误的节点
p != null：说明cur指向第二个错误的节点

找两个节点的两次操作的位置分别对应Morris中序遍历时添加节点到list时操作的位置。这样更方便记忆吧，反正到最后Morris的前中序遍历还是要背的。

public class Solution {
    public void recoverTree(TreeNode root) {
        TreeNode cur = root;
        TreeNode prevNode = null;
        TreeNode p = null;
        TreeNode q = null;

        while (cur != null) {
            if (cur.left == null) {
                if (prevNode != null && prevNode.val >= cur.val) {
                    if(p == null) p = prevNode;
                    q = cur;
                }
                prevNode = cur;
                cur = cur.right;
            } else {
                TreeNode prev = cur.left;
                while (prev.right != null && prev.right != cur) {
                    prev = prev.right;
                }
                if (prev.right == null) {
                    prev.right = cur;
                    cur = cur.left;
                } else {
                    prev.right = null;
                    if (prevNode != null && prevNode.val >= cur.val) {
                        if(p == null) p = prevNode;
                        q = cur;
                    }
                    prevNode = cur;
                    cur = cur.right;
                }
            }
        }
        swap(p, q);
    }

    private void swap(TreeNode p, TreeNode q) {
        if (p == null || q == null) return;
        int temp = p.val;
        p.val = q.val;
        q.val = temp;
    }
}

Morris遍历