Wiggle Sort I & II

• 如何利用单调性

• 怎么 partition

• 什么顺序穿插

• 如何 in-place

看起来像Partition Array又不像的两道题。Google很喜欢这两道。

280. Wiggle Sort

首先这题一看就是要你 O(n) 解的，而且要 in-place，不然毫无挑战，因为 quick sort 都 O(n log n)

这题在条件上，比 Wiggle Sort II 要宽松，因此代码变的可以很简单。

这题还有一个google面经题变种，在这个帖子中，思想非常类似，更利于思考 wiggle sort 的本质

public class Solution {
    public void wiggleSort(int[] nums) {
        if (nums == null || nums.length == 0) return;

        boolean findBigger = true;
        for (int i = 1; i < nums.length; ++i) {
            if (findBigger) {
                if (nums[i] < nums[i - 1]) {
                    swap(nums, i, i - 1);
                }
            } else {
                if (nums[i] > nums[i - 1]) {
                    swap(nums, i, i - 1);
                }
            }
            findBigger = !findBigger;
        }
    }
    private void swap(int[] nums, int a, int b) {
        int tmp = nums[a];
        nums[a] = nums[b];
        nums[b] = tmp;
    }
}

324. Wiggle Sort II

在 Wiggle Sort I 的基础上拿掉了等于号条件，整个题都难了好多，因为这次如果相邻两个数是相等的，怎么 swap 都不符合题意。如果单纯的按顺序扫，就不可避免的会遇到到“找正确元素”的步骤，这个步骤一旦多了，复杂度就上去了。

先写个时间空间复杂度都不对的写法，只要用到了排序，时间复杂度就比O(n)大了。这是一个初步的思路。从后往前依次找剩余元素中最大的，按正序插入数组。

public class Solution {
    public void wiggleSort(int[] nums) {
        if (nums == null || nums.length < 2) return;

        Arrays.sort(nums);
        int[] result = new int[nums.length];
        int index = nums.length - 1;
        for (int i = 1; i < nums.length; --index) {
            result[i] = nums[index];
            i += 2;
        }
        for (int i = 0; i < nums.length; --index) {
            result[i] = nums[index];
            i += 2;
        }
        for (int i = 0; i < nums.length; ++i) {
            nums[i] = result[i];
        }
    }
}

不得不说，Leetcode论坛藏龙卧虎，有个人想了个virtual indexing的方法。

A(i) = nums[(1 + 2*i) % (n | 1)]

(n|1) 强行变奇数。

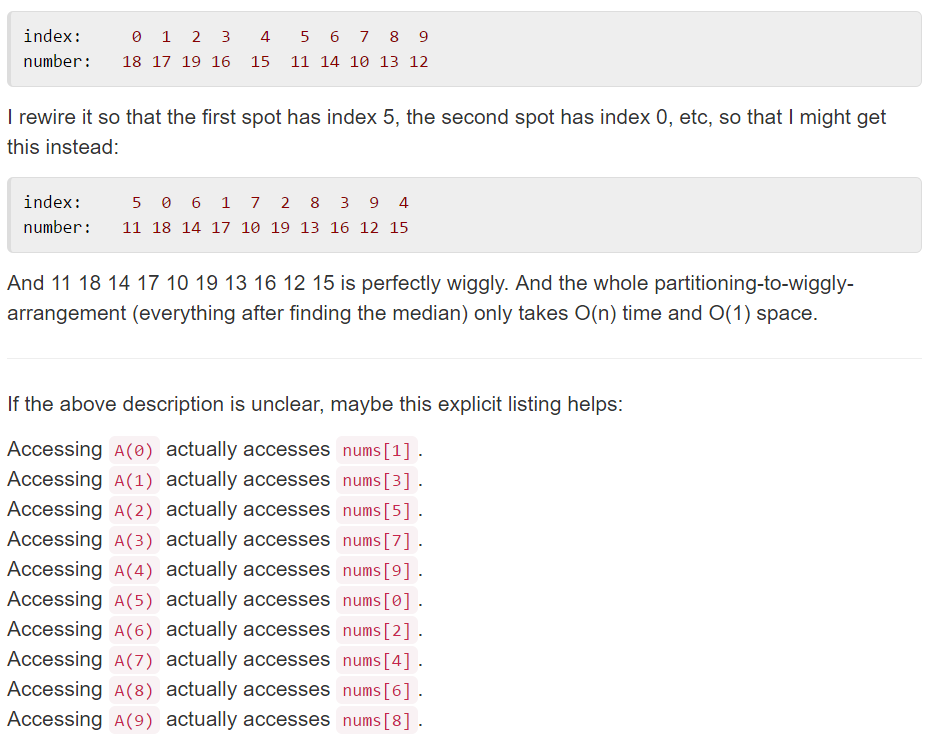
实际上是先用sort colors算法从大到小三分数组，然后找到median再进行virtual indexing。

上面那个 sort 之后从大到小正序穿插插入的顺序，和这题一样，不同之处是，这个写法更符合题目的本质：不需要排序，只需要 partitioning。 正确 partition 的数组只要按照这个顺序插入，都是正确的。median是用findKthLargest那道题的做法去找的。

于是问题就分成了三个子问题：

• 怎么 partitioning

• 什么顺序穿插

• 如何 in-place

public class Solution {
    public void wiggleSort(int[] nums) {
        int median = findKthLargest(nums, (nums.length + 1) / 2);
        int n = nums.length;

        int i = 0;
        int left = 0;
        int right = nums.length - 1;

        while (i <= right) {
            if (nums[newIndex(i, n)] > median) {
                swap(nums, newIndex(left++, n), newIndex(i++, n));
            } else if (nums[newIndex(i, n)] < median) {
                swap(nums, newIndex(right--, n), newIndex(i, n));
            } else i++;
        }
    }
    private int newIndex(int index, int n) {
        return (1 + 2*index) % (n | 1);
    }
    private void swap(int[] nums, int a, int b) {
        int tmp = nums[a];
        nums[a] = nums[b];
        nums[b] = tmp;
    }
}