51. N-Queens

经典的 N 皇后问题，finally。

尝试优化，进行剪枝减少每次需要搜索的格子，比如正解中的后与后之间一定是一个 “马步”，因此只考虑在一个后被放置之后其他的“马步”位置。 然而这样会漏掉一些解，因为一个正解中不是所有后之间都是 “马步” 联系起来的

因此不能单凭“马步”去保证下一个正确的皇后位置，还是要老老实实遍历搜索。

一个比较简单直接的办法是，维护一个 list 代表当前的皇后位置（每一个位置都是valid）在考虑增加新一个王后时，和 list 里已有的每一个皇后比较是否 valid. 问题在于这个 list 的大小是和我们的棋盘大小 n 成正比的，假设一个 list 从0个皇后一直增加到n个皇后，在这个过程中要进行 1 + 2 + 3 ... + n = O(n^2) 次 isValid 操作。

• 45度对角线的 row + column 值是恒等的（一加一减），并且每条对角线的 row + column 值唯一

• 135度对角线的 row - column 值是恒等的（同加同减），并且每条对角线的 row - column 值唯一

• 边长为 n 的棋盘，有 2n - 1 条对角线，并且中间值 (0,0) 的 index 为 n - 1

我们需要需要三个辅助的方法，第一个是DFS的主体程序，第二个是判断是否合法的攻击检测（皇后间是否冲突，第三个是将棋盘画成一个2D matrix返回。

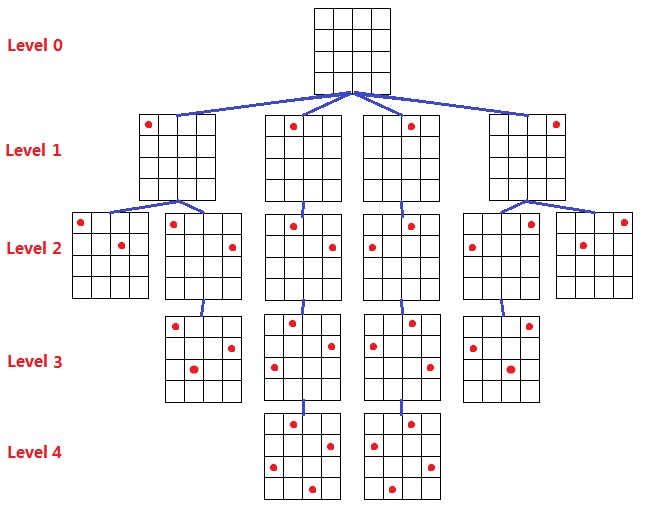
两条对角线判定我推了好久，因为index从0开始和从1开始非常头痛。

• rowIndex + cols.get(rowIndex) == row + column 45度对角线

• rowIndex - cols.get(rowIndex) == row - column 135度对角线

public class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> result = new ArrayList<>();
        if (n == 0) return result;

        List<Integer> list = new ArrayList<>();
        dfs(result, list, n);
        return result;
    }
    private void dfs(List<List<String>> result, List<Integer> cols, int n){
        if (cols.size() == n) {
            List<String> str = drawChess(cols);
            result.add(str);
        }
        for (int colIndex = 0; colIndex < n; ++colIndex) {
            if (!isValid(cols, colIndex)) continue;
            cols.add(colIndex);
            dfs(result, cols, n);
            cols.remove(cols.size() - 1);
        }
    }
    private boolean isValid(List<Integer> cols, int colIndex){
        int row = cols.size();
        for (int rowIndex = 0; rowIndex < row; ++rowIndex) {
            if (cols.get(rowIndex) == colIndex) return false;
            if (rowIndex + cols.get(rowIndex) == row + colIndex) return false;
            if (rowIndex - cols.get(rowIndex) == row - colIndex) return false;
        }
        return true;
    }
    private List<String> drawChess(List<Integer> list){
        List<String> result = new ArrayList<>();
        if (list == null || list.size() == 0) return result;

        for (int i = 0; i < list.size(); ++i) {
            StringBuilder sb = new StringBuilder();
            for (int j = 0; j < list.size(); ++j) {
                if (j == list.get(i)) sb.append("Q");
                else sb.append(".");
            }
            result.add(sb.toString());
        }
        return result;
    }
}

在每步遍历搜索中， 都要 call 一次 isValid() 函数来判断当前格子是否有效，在 dfs + backtracking 的结构不变的情况下，isValid()函数的性能就会成为程序的瓶颈。

一个更取巧的方式是，利用一个皇后会占用这个格子的所有行，列以及对角线的特点，维护所有“行，列，45度对角线，135度对角线” 的 boolean array，这样在每次考虑一个新位置的时候，只需要 O(1) 的时间进行一次操作就可以了。

boolean[] 完全可以，Java 的 BitSet 也不错，不过我实际跑的结果来看，BitSet 在用时上会慢一些，原因在这个帖子：

Boolean-vs-bitset-which-is-more-efficient

boolean[] 一个 boolean 占用大约 1 byte 空间（JVM dependent），BitSet 平均占用 1 bit. boolean[] 的优点是更 CPU efficient, 只有在数组非常大（1000w以上）二者的速度持平。BitSet 内部实现是建立 long[] ，用 64-bit 的块去分配 BitSet 的字节。

• 45度对角线的 row + column 值是恒等的（一加一减），并且每条对角线的 row + column 值唯一, 在 [0,1,2 ... 2n - 2] 区间

• 135度对角线的 row - column 值是恒等的（同加同减），并且每条对角线的 row - column 值唯一，在[-（n-1） ... -2,-1,0, 1, 2 ... n - 1 ] 区间

• 边长为 n 的棋盘，有 2n - 1 条对角线，并且中间值 (0,0) 的 index 为 n - 1

public class Solution {
    public List<List<String>> solveNQueens(int n) {
        boolean[] 
            //ocp0 = new boolean[n], 
            ocp90 = new boolean[n], 
            // 总共 2n - 1 种可能性，(0,0) 的 index 是 n - 1
            ocp45 = new boolean[2 * n - 1], 
            ocp135 = new boolean[2 * n - 1]; 
        List<List<String>> ans = new ArrayList<List<String>>();
        char[][] map = new char[n][n];
        for (char[] tmp : map) Arrays.fill(tmp, '.'); //init

        solve(0, n, map, ans, ocp45, ocp90, ocp135);
        return ans;
    }

    private void solve(int depth, int n, char[][] map, List<List<String>> ans, 
    boolean[] ocp45, boolean[] ocp90, boolean[] ocp135) {
        if (depth == n) {
            addSolution(ans, map);
            return;
        }

        for (int j = 0; j < n; j++)
        // 每次都进行新的一行，所以行不用检查
        // 90度代表棋盘的列
        // 45度对角线（从左上到右下）同一条线上 row + col 是相等的，因此可用作 index
        // 135度对角线（从左下到右上）可从 (0,0) 即 index (n - 1) 为起点
        // 因为同一条对角线 row - col 值恒定，可用作 offset 表示对角线的 index. 
            if (!ocp90[j] && !ocp45[depth + j] && !ocp135[j - depth + n - 1]) {
                ocp90[j] = true;
                ocp45[depth + j] = true;
                ocp135[j - depth + n - 1] = true;
                map[depth][j] = 'Q';

                solve(depth + 1, n, map, ans, ocp45, ocp90, ocp135);

                ocp90[j] = false;
                ocp45[depth + j] = false;
                ocp135[j - depth + n - 1] = false;
                map[depth][j] = '.';
            }
    }

    private void addSolution(List<List<String>> ans, char[][] map) {
        List<String> cur = new ArrayList<String>();
        for (char[] i : map) cur.add(String.valueOf(i));
        ans.add(cur);
    }
}

52. N-Queens II

很可惜，这题解与解之间不存在 optimal substructure 可以有效利用记忆化搜索。老老实实的 DFS + backtracking 还是必要的。

有一些比较妖孽的解法比如 Kunth's 的 Dancing Links，刷题面试的时候，这种大招还是没必要去开了。

既然不需要输出最终解，也就省去了传递 rst 和把棋盘转成 String 的过程。一个问题是，如何在这种dfs + backtracking中维护一个 primitive type 变量，比如有效解的总数？

Java 中默认 primitive type 是 pass by value，而且 Integer type 虽然作为一个 object 存在但是是 immutable, 不能用来作为全局参数多个函数共同更新。

我一直都不喜欢全局变量，感觉用起来太投机取巧了也不好看。

只求解的数量时，可以让 dfs 函数直接返回 int，每次迭代的时候把其他迭代的返回结果加起来就好了。

public class Solution {
    public int totalNQueens(int n) {
        if (n < 2) return n;
        List<Integer> list = new ArrayList<>();

        return dfs(list, n);
    }
    private int dfs(List<Integer> cols, int n) {
        if (cols.size() == n) return 1;

        int count = 0;
        for (int colIndex = 0; colIndex < n; ++colIndex) {
            if (!isValid(cols, colIndex)) continue;
            cols.add(colIndex);
            count += dfs(cols, n);
            cols.remove(cols.size() - 1);
        }
        return count;
    }
    private boolean isValid(List<Integer> cols, int colIndex) {
        int row = cols.size();
        for (int rowIndex = 0; rowIndex < row; ++rowIndex) {
            if (cols.get(rowIndex) == colIndex) return false;
            if (rowIndex + cols.get(rowIndex) == row + colIndex) return false;
            if (rowIndex - cols.get(rowIndex) == row - colIndex) return false;
        }
        return true;
    }
}