拓扑排序
Topological Sorting
连这道题Leetcode都没有,我真的有点醉了。
BFS的方法,很简单。
无论是 directed 还是 undirected Graph,其 BFS 的核心都在于 "indegree",处理顺序也多是从 indegree 最小的开始,从外向内。
我们先用一个 HashMap 统计下所有节点的 indegree; 值越高的,在拓扑排序中位置也就越靠后,因为还有 N = current indegree 的 parent node 们没有处理完。
因此在循环最开始,我们可以把所有 indegree = 0 (也即不在 hashmap 中) 的节点加到 list 中,也作为 BFS 的起点。
在 BFS 过程中,我们依次取出队列里取出节点 node 的 neighbors, next,并且对 next 对应的 indegree -1,代表其 parent node 已经被处理完,有效 indegree 减少。
当-1之后如果 next 的 indegree 已经是 0 , 则可以加入 list,并且作为之后 BFS 中新的起始节点。
从 Course Schedule 的 BFS 做法学到的经验是,如果图中有环,会有环上的 node 永远无法减到 indegree = 0 的情况,导致一些 node 没有被访问。
这也是当初面试被问到的为什么 JVM 不只靠 reference counting 来做 GC,就是因为有环的时候,indegree 不会减到 0.
public class Solution {
public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
ArrayList<DirectedGraphNode> result = new ArrayList<>();
if (graph == null || graph.size() == 0) return result;
Map<DirectedGraphNode, Integer> map = new HashMap<>();
for (DirectedGraphNode node : graph) {
for (DirectedGraphNode neighbor : node.neighbors) {
if (map.containsKey(neighbor)) {
map.put(neighbor, map.get(neighbor) + 1);
} else {
map.put(neighbor, 1);
}
}
}
Queue<DirectedGraphNode> queue = new LinkedList<>();
for (DirectedGraphNode node : graph) {
if (!map.containsKey(node)) {
result.add(node);
queue.offer(node);
}
}
while (!queue.isEmpty()) {
DirectedGraphNode node = queue.poll();
for (DirectedGraphNode n : node.neighbors) {
map.put(n, map.get(n) - 1);
if (map.get(n) == 0) {
result.add(n);
queue.offer(n);
}
}
}
return result;
}
}
DFS做法
CLRS 上图论的一小节。给定一个有向图,在拓扑排序中可以有很多个正确解,由若干小段的 list 组成。但是要保证:
正确的单序列顺序(具体一个 list 之间的元素)
正确的全序列顺序(所有的 lists 之间)
以下图为例,不论先从哪个点开始 DFS,例如 dfs(belt)会得到一个 belt -> jacket 的 list; 但同时因为 pants -> belt,在最终的结果中,包含 pants 的 list 要排在包含 belt 的 list 前面。
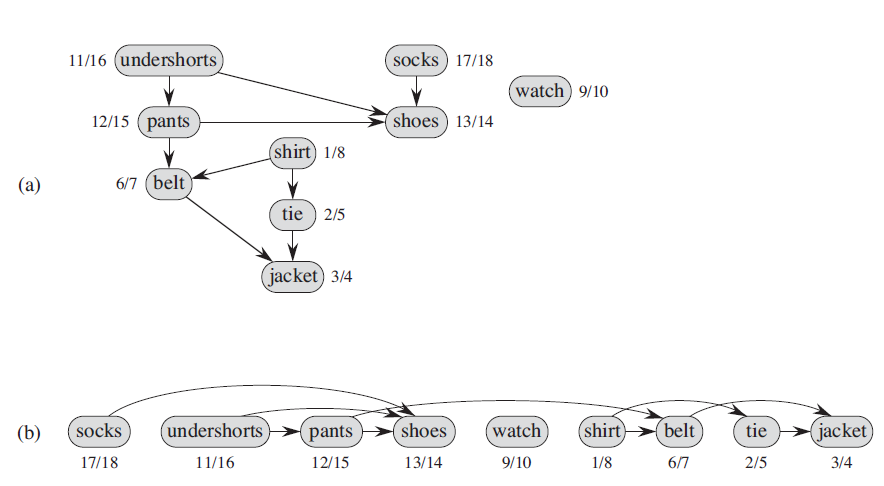

CLRS 上的算法是,每次 DFS 得到一个符合正确拓扑顺序的 list,保证单序列顺序;每次新的 DFS 之后得到的 list 要排在之前结果的前面,保证全序列顺序。
我的写法是,每次 DFS 得到一个相反顺序的 list; 新的 DFS 返回 list 排在之前结果的后面; 最后把整个 list 翻转,思路类似于 类似于 reverse words in string (正单序列,反全序列),或者 Rotate Array (正单序列,反全序列)里面的多步翻转法。
每次翻转都会改变单序列 & 全序列之间的顺序,对于每一个单序列或者全序列,两次翻转可以互相抵消。
这个思路体现在多步翻转法上就是依次翻转每个单序列,最后全部翻转,因而单序列顺序不变,全序列顺序翻转。
而我这题一开始就是“反单序列” 和 “反全序列”,因此一次完全翻转之后就可以得到“正单序列” 和 “正全序列”。
public class Solution {
public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
// write your code here
ArrayList<DirectedGraphNode> list = new ArrayList<DirectedGraphNode>();
HashSet<DirectedGraphNode> set = new HashSet<DirectedGraphNode>();
for(DirectedGraphNode root : graph){
if(!set.contains(root)) dfs(list, set, root);
}
// 现在的 list 是由若干个顺序倒转的 topological order list 组成的
// 这里的处理类似于 reverse words in a string
// 把每个单词单独翻转之后,再把整个句子翻转
Collections.reverse(list);
return list;
}
private void dfs(ArrayList<DirectedGraphNode> list,
HashSet<DirectedGraphNode> set,
DirectedGraphNode root){
set.add(root);
for(DirectedGraphNode node : root.neighbors){
if(!set.contains(node)) dfs(list, set, node);
}
// 到这一步,root 节点的所有 sub path 都已经被访问过了
// 最后才在 list 中添加元素,得到的是一个反序的 topological order
list.add(root);
}
}
做了欧拉回路之后,发现一个更好的做法是直接建 LinkedList,然后用 addFirst();
熟练使用 API 很重要啊
public class Solution {
public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
// write your code here
LinkedList<DirectedGraphNode> list = new LinkedList<DirectedGraphNode>();
HashSet<DirectedGraphNode> visited = new HashSet<DirectedGraphNode>();
for(DirectedGraphNode root : graph){
dfs(list, root, visited);
}
return new ArrayList<DirectedGraphNode>(list);
}
private void dfs(LinkedList<DirectedGraphNode> list, DirectedGraphNode root, HashSet<DirectedGraphNode> visited){
if(visited.contains(root)) return;
for(DirectedGraphNode next : root.neighbors){
dfs(list, next, visited);
}
list.addFirst(root);
visited.add(root);
}
}